|
FISICA DELLE ONDE
UNA FRECCIA ROTANTE
La figura mostra un punto P che gira lentamente su una
circonferenza in senso antiorario.
Al posto del punto possiamo visualizzare un vettore ovvero
una "freccia rotante" OP (come la lancetta di un orologio).
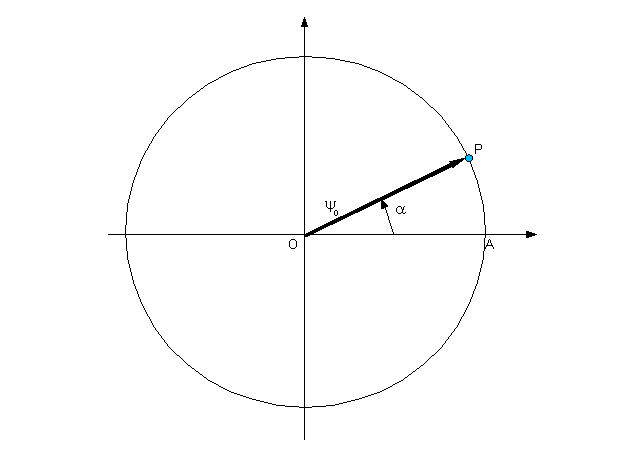
Perché la freccia gira in
senso antiorario ? Mah , è una scelta arbitraria tanto per
scegliere un verso e per misurare l'angolo α (alfa), detto
"angolo di fase" ovvero semplicemente "fase", a partire da
un'origine arbitraria A.
Il punto gira e la fase α aumenta, il punto ripassa su A e
la fase α riparte da zero, gira e gira e ogni volta che il
punto passa per A tutto si ripete come prima in modo
monotono (mi raccomando, non ti addormentare).
Si dice che il moto osservato è "periodico".
Osservando il punto non si può stabilire da quanto tempo
giri .... forse da sempre.
Se lo bloccassimo potremmo misurare l'angolo di fase α ma
che ore sono veramente ? Questo orologio misura solo la fase
α. In quale delle innumerevoli volte in cui questa fase è
stata raggiunta mi trovo ora ?
Abbiamo l'impressione che qualcosa accada ma stiamo
veramente vivendo nel tempo?
FREQUENZA E INDETERMINAZIONE TEMPORALE
Vediamo di catturare questo punto, di descrivere come
gira.
Intanto potrei dire che la circonferenza ha un raggio di
lunghezza ψ0 (pronuncia: psi con zero) che
chiamiamo "modulo".
Ora mi manca qualcosa che descriva la velocità di rotazione
del punto.
Potrei cogliere il momento in cui il punto passa per A,
aspettare un po di tempo contando il numero di giri in un
secondo e chiamare il risultato "frequenza", unità di
misura: giri al secondo ovvero Herz.
"Se il punto gira lentamente cosa ci faccio con un secondo ?
Per contare il numero di giri è meglio aspettare un minuto.
Anzi, per aumentare la precisione sarebbe meglio aspettare
un'ora. Più aspetto e più precisa è la conta" .
Ed ecco il "principio di indeterminazione". Pensate che
ancora ci sono fior di fisici che vanno dicendo che si
tratta di un concetto che prescinde dal comune buon senso.
In sostanza il ragionamento è questo : se tu prendi una
immaginaria macchina fotografica e fai un flash sul punto
ruotante hai congelato un bel pò di informazioni. Sai
l'istante di tempo esatto in cui hai preso la foto e dalla
foto puoi ricavare il modulo e la fase della freccia che
ruota ma dalla foto non puoi determinare la frequenza. La
frequenza è totalmente indeterminata con questo esperimento.
Viceversa se fai un altro esperimento, aspetti un'ora e
conti 521 giri , sei abbastanza preciso sulla frequenza ma
non puoi rispondere alla domanda : " In che istante ho
misurato la frequenza ? "
In un esperimento o è determinato l'istante di tempo od è
determinata la frequenza ma non tutte e due
contemporaneamente.
Nella definizione di frequenza c'è qualcosa di sottile che
prescinde dal tempo.
La frequenza "istantanea" non ha senso, non è una variabile
fisica.
Aggiungo un particolare tecnico. I fisici amano misurare la
frequenza in angoli (radianti) al secondo, indicarla con la
lettera greca omega ω e chiamarla "pulsazione". Si tratta
concettualmente sempre della stessa cosa quindi da questo
momento considereremo analoghe frequenza e pulsazione.
La comodità di lavorare con la pulsazione ω è che esiste una
semplice relazione fra ω, l'intervallo di tempo t (da ora in
poi il delta è sottinteso) e la fase α accumulata
nell'intervallo di tempo :
α = ω t
Questa formula ovvia e
semplicissima è di una importanza inimmaginabile e bisogna
osservarla e ricordarla.
Esempio: se la pulsazione ω
= 3 radianti/sec in un tempo t = 2 sec si accumula un angolo
di fase α = 2 x 3 = 6 radianti. Banale no?
Faremo ancora un lungo giro per i meandri della fisica e
quando ritroveremo questa formula saremo alla fine di questi
appunti.
Come sempre la verità è davanti agli occhi e non la vediamo.
OSCILLATORE
Adesso aggiungiamo un particolare al nostro disegno:
C'è un nuovo asse sulla destra e su di esso viene proiettato
il moto circolare del punto P. Con un solo asse abbiamo
perso una dimensione e adesso il punto P oscilla su e giù
tra M e N con un movimento strano, irregolare.
Mentre prima P si muoveva a velocità costante sulla
circonferenza, la sua proiezione va più veloce quando si
trova nei pressi di A mentre in M e N rallenta e sembra
fermarsi un attimo prima di cambiare verso.
Mentre prima il modulo OP era costante adesso l'ampiezza
dell'oscillazione AP varia da zero al modulo AM e cambia
anche di segno quando passa sotto l'origine A.
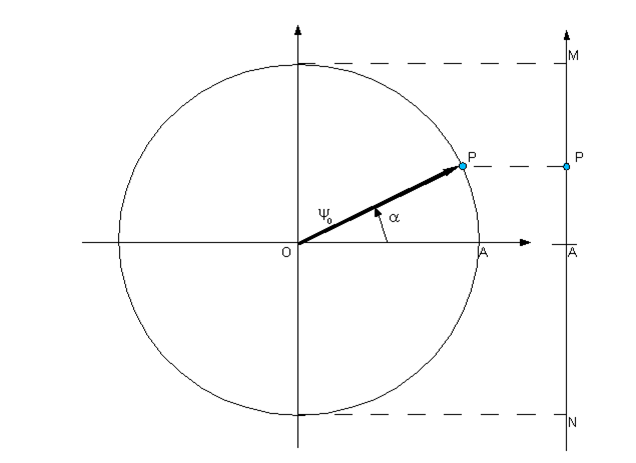
Sono gli scherzi delle dimensioni :
quando la tua visuale si restringe il mondo ti sembra più
strano e meno armonico.
Visto che il punto P ora oscilla, chiameremo il nuovo
oggetto "oscillatore".
Ci sono molti oscillatori in giro ? Moltissimi, credimi.
Una comune altalena, un pendolo, la corda di un violino, una
barca in un mare ondoso, il moto dei pianeti e così via
all'infinito.
Ti presento un oscillatore che pulsa ad una frequenza folle:
l'elettrone pulsa a 120.000.000.000.000.000.000 Herz .
Che senso ha la nostra percezione del tempo per questo
oscillatore ?
Visto che si tratta di una frequenza assurda , la
percepiamo come energia interna o meglio come massa
dell'elettrone.
SINUSOIDE TEMPORALE
Aggiungiamo un ultimo particolare.
Attaccata al punto oscillante adesso c'è una penna che
scrive su una striscia di carta che scorre uniformemente
verso destra: una registrazione su carta del moto
dell'oscillatore.
La penna va su e giù e la carta scorre da sinistra a destra.
.png)
Tempo
Chiaramente nel grafico
sulle ascisse c'è il tempo (magari in secondi) e in ordinate
l'oscillazione della penna .
La figura che viene fuori è molto sofisticata ed elegante:
si chiama "sinusoide temporale".
Anche la sinusoide ha le stesse caratteristiche
dell'oscillatore: l'ampiezza oscilla come l'ampiezza
dell'oscillatore, la frequenza è facilmente deducibile dal
diagramma contando le figure che si ripetono in un certo
tempo, la differenza di fase è anch'essa facilmente
deducibile.
Notiamo che la sinusoide temporale assomiglia ad un'onda ma
non è un'onda, è una registrazione.
SOMMA DI OSCILLATORI
Andiamo subito ad osservare l'importanza della fase (angolo
di fase).
In fisica classica uno più uno fa due. Sommando una mela a
un'altra mela si hanno due mele.
Ma se il mondo è fatto di vettori ruotanti od oscillatori
questo non è più vero.
La somma di oscillatori si chiama interferenza.
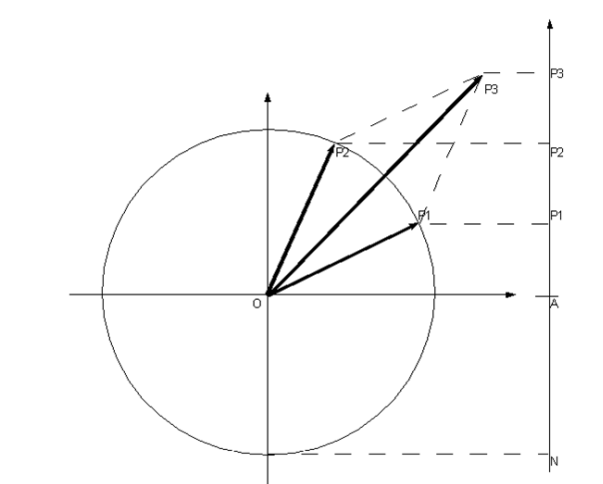
Nella figura sopra i
vettori sono due : P1 e P2. Supponiamo che il modulo di
ognuno di essi valga uno.
La somma di vettori si fa con la regola del parallelogramma:
P3 = P1 + P2 (ricorda quanto studiato a scuola a proposito
della somma di forze).
E' quindi chiaro che il modulo di P3 dipende dalla posizione
dei due vettori P1 e P2 (si dice che dipende dallo
sfasamento o differenza di fase fra P1 e P2). Se P1 e P2
fossero opposti l'uno all'altro (si dice in opposizione di
fase) la loro somma sarebbe zero. Se P1 e P2 sono
sovrapposti la loro somma fa due.
Nel mondo dei vettori e delle onde uno più uno può quindi
fare un numero da 0 a 2 a seconda della differenza di fase
fra i due vettori. Questo fatto produce molti casi diversi
che andiamo ad osservare.
Stessa frequenza
P1 e P2 sono due vettori che ruotano alla stessa velocità
(ovvero hanno la stessa frequenza) e quindi il loro
sfasamento si mantiene costante.
La loro somma è un oscillatore che pulsa ancora alla stessa
frequenza. E' un po come due persone che si intendono. Il
risultato della loro discussione è comprensibile: se poi
tirano dalla stessa parte il risultato (il modulo del
risultato, in rosso nelle due figure che seguono) può essere
vicino a due (si chiama "interferenza costruttiva", prima
figura), se tendono a tirare in direzione opposta il
risultato è vicino a zero (si chiama "interferenza
distruttiva", seconda figura).
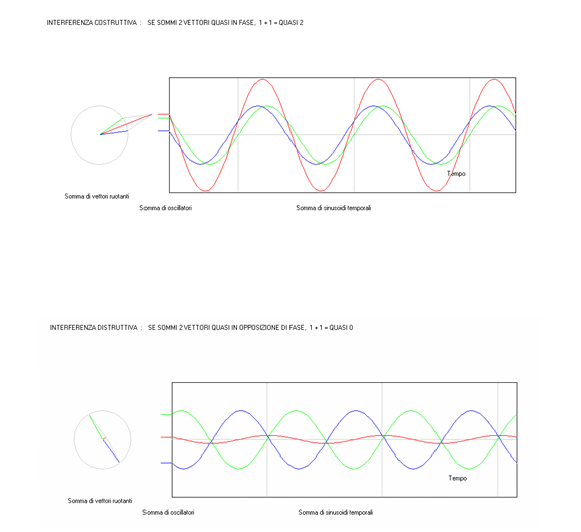
Frequenza diversa
Vediamo il caso di due vettori che girano a frequenza
diversa . La loro somma non è stabile e il punto ruotante
somma non descrive un cerchio ma una spirale.
La registrazione della somma non è più una sinusoide, forse
non è neanche una figura periodica e quindi non ha una
frequenza e neanche una fase. In altri termini è un
risultato apparentemente con poco senso.
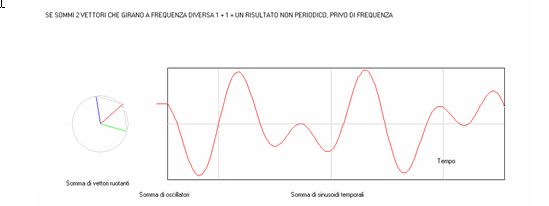
La difficoltà si accentua
se i vettori ruotanti a frequenze diverse sono molti. In
questo caso la somma è uno sgorbio insensato e lo percepiamo
come rumore.
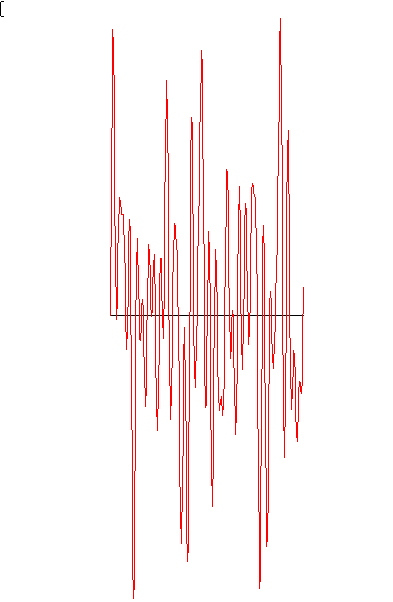
Il rumore in natura esiste
ed è frequentissimo ma per fortuna ha la caratteristica di
essere basso perchè l'interferenza di molte onde, diverse
fra loro, finisce (per ragioni statistiche) per produrre
mediamente un risultato quasi nullo.
Attenzione: ho detto "quasi". Non è possibile
statisticamente ottenere dalla confusione totale un
risultato perfettamente nullo.
In Natura il nulla non esiste. Esiste un leggero rumore di
fondo, somma di innumerevoli fenomeni.
Il nostro cervello impara dalla nascita ad estrarre qualche
informazione ed eliminare il resto. Vengono eliminati i
rumori nei suoni, nelle visioni, nei ricordi, nelle idee.
Gli uomini ingegnosi fanno di più e riescono a tirar fuori
le cose essenziali dal rumore superfluo. Vengono estratte
informazioni finché il cervello ce la fa a cercare il senso
delle cose.
Battimento
C'è un caso particolare in cui la somma di sinusoidi a
frequenza diversa sembra avere senso: le due frequenze sono
molto vicine . Si ottiene una misteriosa figura detta
battimento apparentemente periodica.
|
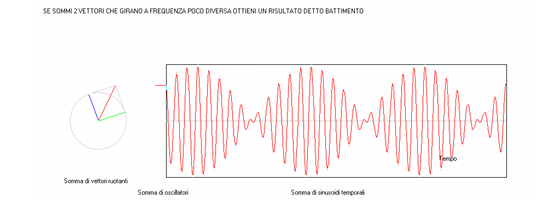 |
Chi la osserva percepisce
due frequenze. La frequenza più alta (i picchi vicini)
coincide con quella media delle due sinusoidi iniziali, la
seconda è più bassa (i gruppi di onde che si ripetono) e
corrisponde alla semidifferenza di frequenza fra le due
sinusoidi sommate.
Ad esempio se la prima prima sinusoide ha frequenza 102 Hz e
la seconda ha frequenza 100 Hz, otteniamo un battimento con
alta frequenza di (100+102)/2 = 101 Hz mentre la bassa
frequenza del battimento è (102-100)/2 = 1 Hz.
Questa misteriosa figura assomiglia ad una serie di
scariche. Ogni scarica inizia con rapidissime vibrazioni
prima crescenti e poi decrescenti.
Credo che la tua sensibilità si sia allertata alla vista del
battimento.
Hai ragione: è un fenomeno a cui dobbiamo prestare
attenzione in particolare quando viene associato all'effetto
Doppler di cui parleremo fra poco.
IL MONDO DEGLI SPETTRI
Nel mondo reale gli oscillatori a frequenze diverse si
sprecano e abbiamo visto che la loro interferenza assomiglia
più ad un rumore che ad una cosa sensata.
Adesso vogliamo un modo razionale per analizzare il rumore.
La rappresentazione attraverso frecce rotanti non è un gran
che perché esse si rincorrono, si superano e si sommano in
modo sempre diverso.
Ma non c'è proprio modo di descrivere un complesso di
oscillatori a diversa frequenza ? Beh un modo c'è ed è stato
inventato da un grande matematico, ingegnere e filosofo
francese, che visse ai tempi della rivoluzione e per un pelo
non fu ghigliottinato da Robespierre (non andò così bene al
padre della chimica Lavoisier preso di mira da Marat).
Fourier (1768-1830) costruì
una teoria complessa e misteriosa con risvolti filosofici
profondissimi.
Noi per formarci un'immagine guarderemo la figura seguente
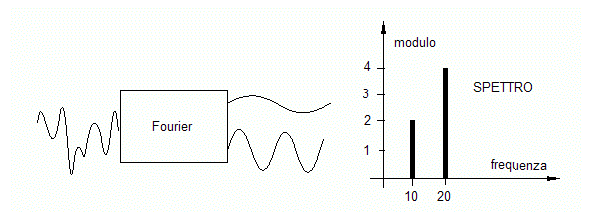
Da sinistra un rumore entra
nella macchina matematica di Fourier (detta trasformata di
Fourier) che funziona da filtro. Dall'altra parte escono ben
distinte le sinusoidi che compongono il rumore.
Con queste sinusoidi si costruisce un grafico, detto
"spettro" che mette in evidenza le caratteristiche delle
sinusoidi selezionate cioè la frequenza, l'ampiezza e la
fase (non mostrata in figura).
Per esempio lo spettro mostrato si legge così : abbiamo
messo nel paniere due sinusoidi, una con frequenza 10 e
ampiezza 2, l'altra con frequenza 20 e ampiezza 4. Una bella
comodità per dare un senso al rumore !
Ma c'è molto di più: se
dentro scatola di Fourier mettiamo un sistema fisico
(lineare) e lo sollecitiamo dall'esterno, Fourier ci informa
che la conoscenza dello spettro corrisponde ad una
conoscenza completa della dinamica del sistema del tutto
sostituibile con la conoscenza delle equazioni che lo
governano. In altri termini, pur non sapendo cosa abbiamo
messo dentro la scatola di Fourier, siamo in grado di
calcolare con precisione come tale sistema si comporterà. La
conoscenza dello spettro equivale ad avere studiato il
sistema in esame ed avere trovato un modello matematico che
lo rappresenti.
Questa scoperta è veramente sconvolgente dal punto di vista
filosofico.
Al limite potremmo pensare che la fisica possa andare avanti
senza saper nulla del mondo reale ma raccogliendo spettri e
prevedendo con esattezza quello che sta per accadere. Gli
spettri possono diventare il condensato della nostra
conoscenza del mondo specialmente quando i sistemi diventano
così piccoli da essere inaccessibili come nella fisica delle
particelle.
Se la trasformata di Fourier è la porta che immette dallo
spaziotempo al mondo degli spettri, Fourier costruì anche la
porta per uscirne (antitrasformata di Fourier) ma è
piuttosto stretta per cui accade che chi entra nel mondo
degli spettri spesso ci rimanga.
La gente che lavora con gli spettri dopo un po subisce una
strana metamorfosi: si comporta come se il tempo non
esistesse ed al suo posto ci fossero solo le frequenze. Il
mondo degli spettri è utile e stranamente sta in piedi
anche senza il
tempo.
La nostra ψ è una
frequentatrice assidua di questo mondo senza tempo.
ONDE PROGRESSIVE
Adesso poniamo un oscillatore nello spaziotempo. Cosa accade
? Qualcosa si propaga in tutte le direzioni.
Per agevolare la
comprensione facciamo una approssimazione. Facciamo finta
che lo spazio non abbia 3 dimensioni ma una sola, cioè non
sia un volume ma una linea orizzontale.
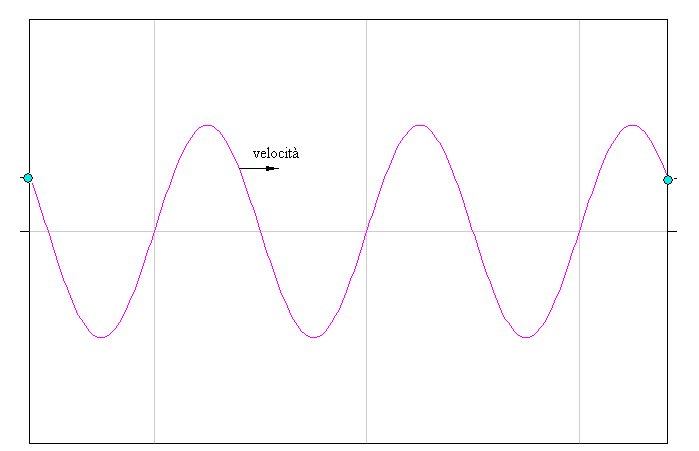
Guardando notiamo che la
cosa che si propaga assomiglia ad una sinusoide ma ora non è
più una sinusoide temporale, E' come un oggetto rigido in
fil di ferro che si muove lentamente da sinistra a destra
sullo sfondo fermo.
Si chiama "onda progressiva".
L'onda progressiva di ψ è il mattone della fisica
quantistica. Ogni minuto perso a vederla scorrere è un
minuto guadagnato.
Nota che la figura sembra la stessa di quella
dell'oscillatore di prima ma adesso le righe verticali sono
ferme e l'onda progressiva si muove rispetto allo sfondo.
La distanza fra due righe verticali non è più un secondo ma
un metro.
La figura sopra potrebbe rappresentare la fotografia
dell'onda progressiva scattata in un certo istante, un'onda
progressiva ferma che chiamiamo "sinusoide spaziale".
Bene, che cosa si può misurare di questa sinusoide spaziale
? Due cose : una è la solita ampiezza con valore massimo
uguale al modulo ψ0 l'altra è il numero di cicli
al metro.
Il numero di cicli al metro è una quantità molto importante
e si chiama "numero d'onde" (qualche volta viene riferito il
suo inverso che è la "lunghezza d'onda").
Si tratta dell'esatto corrispondente della frequenza
dell'oscillatore ma c'è lo spazio al posto del tempo.
E' chiaro che la frequenza ed il numero d'onde si integrano
nel concetto di onda progressiva e questo è importante.
Adesso torniamo alla fotografia dell'onda progressiva.
Posso stabilire il momento in cui ho scattato la foto ma
posso anche dire in che punto dello spazio si trova l'onda ?
Ebbene no. Solo l'istante e il numero d'onde.
Allora completiamo il cosiddetto principio di
indeterminazione .
"La frequenza è compatibile con la posizione ma non col
tempo, il numero d'onde è compatibile con il tempo ma non
con la posizione".
Come vedi il principio di indeterminazione non è un arcano
incantesimo inventato dalla fisica quantistica: tutti i
fenomeni caratterizzati da onde lo subiscono.
La funzione di quest'onda
progressiva è di mettere in contatto due oscillatori alla
stessa frequenza e più precisamente di stabilire una
relazione fra le fasi di due oscillatori per cui le daremo
un nome significativo : "propagatore".
CONDIZIONI AL CONTORNO
Se guardiamo bene la figura dell'onda progressiva, notiamo
che gli oscillatori sono due, uno a sinistra e uno a destra
e che il primo emette l'onda progressiva mentre il secondo
la assorbe e la subisce.
L'operazione si chiama "accoppiamento". Il primo oscillatore
sulla sinistra lo chiamiamo "emettitore" il secondo sulla
destra "ricevitore".
L'equivalente meccanico di questo fenomeno è un buon
portiere che afferra saldamente una palla assorbendo col suo
corpo tutta l'energia.
Tuttavia non tutti i ricevitori sono uguali e quindi non
tutti gli accoppiamenti sono simili.
Ad esempio il ricevitore potrebbe ignorare l'onda
progressiva come un portiere che manca la palla. In questo
caso l'onda progressiva proseguirebbe indisturbata senza
cedere alcuna energia.
La palla potrebbe altresì colpire il palo della porta ed
essere riflessa all'indietro anche questa volta senza cedere
alcuna energia (il palo l'ha restituita elasticamente).
Sono possibili tanti casi intermedi come il portiere che
prende la palla ma, non riuscendo ad assorbire tutta
l'energia, se la lascia sfuggire.
Addirittura potremmo avere un portiere che blocca la palla,
si guarda attorno e quindi la calcia nuovamente in una
qualunque direzione.
Tutte queste combinazioni, si chiamano "condizioni al
contorno" dell'equazione differenziale delle onde e sono
importanti per stabilire che fine farà l'onda.
Potrebbe sembrare facile stabilire volta per volta le
condizioni al contorno di un problema ma ce ne sono alcune,
ad esempio al centro di un elettrone, che sono un vero
rompicapo e costituiscono la frontiera della fisica.
PROPAGATORE NON LOCALE
Adesso dobbiamo affrontare il problema più misterioso della
meccanica quantistica su cui torneremo in seguito : il
propagatore non locale.
Visto che si tratta di una cosa importante riporto una
figura esplicativa.
Supponiamo che un'onda progressiva (o propagatore), come
quelle che abbiamo già osservato, porti informazioni (su
frequenza, fase ed ampiezza) da un oscillatore A in un punto
dello spazio ad un oscillatore B in un altro punto dello
spazio (vedi figura denominata PRIMA).
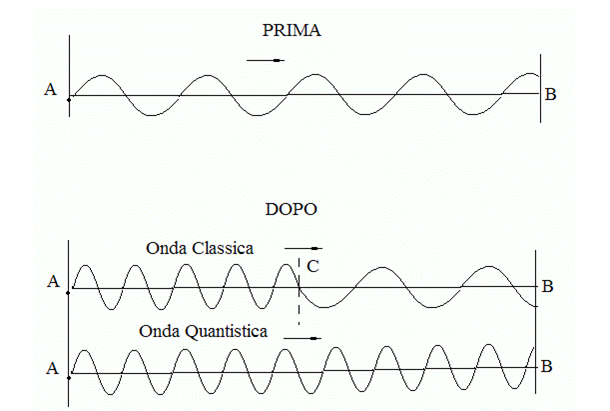
Metti che ad un certo istante l'oscillatore A aumenti la sua
frequenza di vibrazione (vedi figura denominata DOPO).
Nel caso di un'onda classica questa informazione si propaga
con un fronte d'onda (punto C) ad una certa velocità
inferiore o uguale a quella della luce per cui l'oscillatore
B deve attendere un periodo più o meno lungo prima di
venirne a conoscenza. Alla sinistra del fronte C di
propagazione l'onda vibra ad alta frequenza mentre a destra
vibra ancora a bassa frequenza.
Al contrario un'onda non locale si adegua immediatamente
alla nuova frequenza ed istantaneamente ne informa
l'oscillatore B anche se questo è distante milioni di anni
luce. Non esiste un fronte d'onda in moto. Attraverso il
propagatore tutto l'universo è in presa diretta !
Fenomeni analoghi sono stat rilevati cambiando la condizione
al contorno in B. Immediatamente l'onda su tutto il
percorso si adegua.
Sembra che il mondo degli spettri di Fourier abbia trovato
modo di insinuarsi nel mondo reale e ci propone fenomeni
fuori dal tempo.
Se ci fai caso un'onda
atemporale è più semplice da studiare e non è difficile da
immaginare. Infatti siamo abituati a pensare ad effetti
istantanei quando ci muoviamo nel nostro ambito domestico.
Ad esempio se giri l'interruttore sembra che istantaneamente
si accenda ovunque la luce.
Bene: un propagatore non locale accende istantaneamente la
luce in tutto l'universo. Come poi faccia veramente non è
affatto ovvio nè attualmente c'è modo di sfruttare
praticamente questa possibilità di trasmissione istantanea
delle informazioni.
Tuttavia ci provano in tanti e prima o dopo...
ONDE STAZIONARIE
Spesso l'onda progressiva emessa da un oscillatore (onda
diretta) incontra un ostacolo e viene riflessa in direzione
opposta senza scambio di energia.
L'onda riflessa si somma all'onda diretta e il risultato è
sorprendente.
Si chiama "onda stazionaria" e non si muove. Pulsa e non si
muove.
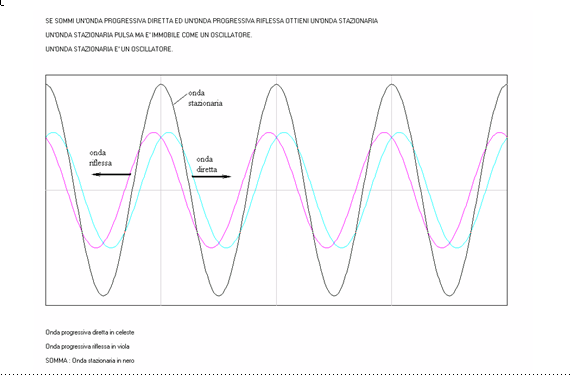
Osserva attentamente il
programma ONDE sommando punto per punto il valore dell'onda
diretta e quella riflessa.
Credo che con l'intuito scoprirai perché la somma non si
muove nello spazio.
Per me la prima volta è stata un'emozione.
Infatti noi sappiamo già che qualcosa che pulsa e non si
muove è un oscillatore.
Bene, l'onda stazionaria è un oscillatore esteso in un certo
spazio (piccolo come una particella o grande come
l'universo).
Così il cerchio si chiude:
Siamo partiti da un oscillatore fermo e abbiamo scoperto che
nello spaziotempo emette onde progressive.
Ora abbiamo scoperto che la somma di onde progressive
dirette e riflesse da certe condizioni al contorno appare
come un oscillatore fermo.
Morale: non c'è niente di fermo, l'oscillatore sembra fermo
ma in realtà ha una struttura interna in cui onde
progressive dirette e riflesse si sommano dando
l'impressione dell'immobilità.
Gli unici componenti del nostro panorama rimangono lo
spazio, il tempo (o lo spaziotempo) e le onde progressive.
L'UNIVERSO QUANTIZZATO
|
 |
L'altalena è un oscillatore
e non può che oscillare ad una "frequenza propria" che
dipende solo dalla lunghezza della corda (parola di Newton).
Per quanto la ragazza si agiti non può cambiare la frequenza
propria dell'altalena né una gradevole spinta di un forzuto
ammiratore può avere miglior fortuna.
Se queste spinte fossero sincronizzate con la frequenza
propria si avrebbe un effetto vistoso : l'altalena andrebbe
in "risonanza" amplificando l'oscillazione.
Se invece queste spinte fossero date con una frequenza
diversa, l'effetto sarebbe smorzato fino quasi a fermare
l'altalena.
Se però il forzuto agisse con pazienza e provasse una
frequenza dopo l'altra, l'altalena si comporterebbe come un
filtro: ignorerebbe le spinte alle frequenze sbagliate e si
gioverebbe dell'unica giusta per assorbire energia e andare
in risonanza.
Ti chiedi: ma se l'altalena è ferma, ha ugualmente una
frequenza propria ?
Risposta : si, la frequenza propria dipende dalla lunghezza
della corda, è una caratteristica del sistema altalena e non
dipende dal fatto che in questo momento ci si dondoli o
meno.
Questo fatto è importante e fa della frequenza propria
qualcosa di strutturale e tuttavia ipotetico, non
necessariamente in atto.
Come già ti ho accennato il mondo delle frequenze e degli
spettri vive in qualche modo fuori dal tempo.
Fuori dal tempo sarà infatti lo spettro dell'altalena: in
ascisse mettiamo la frequenza (o la pulsazione) che il
forzuto di volta in volta prova e in ordinate mettiamo
l'effetto ottenuto.

Come vedi a quasi tutte le
frequenze ω l'effetto è quasi nullo ma quando ci
si avvicina alla frequenza propria l'effetto cresce fino ad
un massimo per poi diminuire.
Questa può essere una sorpresa. Ci saremmo magari aspettati
che l'altalena rispondesse solo alla frequenza propria (solo
una riga verticale nello spettro) ma ora vediamo che
risponde con una certa indeterminazione in una zona attorno
alla frequenza propria.
Poco fa, parlando del filtro matematico di Fourier ho
commesso una imprecisione: lo spettro non è mai a barre,
ogni picco assomiglia a una curva di Gauss più o meno
allargata. Quindi anche i filtri matematici introducono una
indeterminazione nello spazio e nel tempo, non si tratta di
imprecisione della misura nè l'onda di per se ha una
frequenza imprecisa, l'indeterminazione si crea quando
un'onda interagisce con qualunque cosa.
Abbiamo osservato che l'oscillatore emettitore e
l'oscillatore ricevitore per essere accoppiati devono avere
la stessa frequenza di risonanza proprio come l'ammiratore e
l'altalena. Se la frequenza di eccitazione non è la stessa
della frequenza di risonanza l'oscillatore ricevitore
semplicemente ignorerà l'onda in arrivo come il portiere che
manca la palla.
Questo comportamento dell'oscillatore ricevitore fa si che
esso stesso possa essere utilizzato come filtro.
Ad esempio se
mandi la luce bianca del sole, che possiede una miscela di
frequenze ossia di colori, attraverso una atmosfera che
assorbe e riemette il blu, vedrai un cielo blu e così via
per tutti i colori di tutti gli oggetti. D'altra parte la
luce diretta del sole, privata del blu apparirà più rossa
specialmente al tramonto quando gli strati di aria da
attraversare sono più spessi.
C'è un'altra
possibilità di utilizzo del ricevitore come strumento di
misura della frequenza. Se l'ammiratore-emettitore avesse
solo una frequenza a disposizione (un tipo poco elastico),
la ragazza-ricevitore potrebbe, allungando e accorciando la
corda dell'altalena, cercare di uguagliare la frequenza di
risonanza dell'altalena alla frequenza dell'emettitore e
quindi realizzare ugualmente l'accoppiamento. A questo punto
la lunghezza della corda potrebbe essere presa come una
misura della frequenza dell'emettitore.
Più o meno il filtro matematico di Fourier funziona allo
stesso modo.
Se, come sembra, tutto l'universo è
fatto di oscillatori, qualunque misura è naturalmente
indeterminata.
L'OSCILLATORE
DISTRIBUITO NELLO SPAZIO
Lasciamo l'altalena e torniamo all'oscillatore : l'onda
stazionaria, somma di un'onda progressiva diretta e una
riflessa.
Ci potremmo aspettare che l'ostacolo che ha riflesso
quell'onda non sia solo alla nostra destra ma ce ne sia uno
anche a sinistra, pronto anche lui a rimbalzare indietro
l'onda riflessa.
In generale il numero di riflessioni in mancanza di perdite
è infinito.
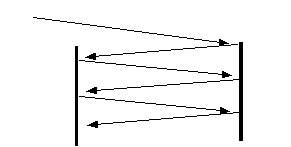
Come abbiamo già visto,
ogni coppia di onde (una diretta e una riflessa) determina
un'onda stazionaria quindi in questa specie di scatola
avremo una infinità di onde stazionarie cioè una infinità di
oscillatori tutti alla stessa frequenza ma sfasati fra di
loro.
Osserviamoli con il sistema dei vettori ruotanti: una
freccia per ogni oscillatore (quindi per ogni coppia di
onde).
Come vedi dalla figura queste frecce, pur girando alla
stessa frequenza, hanno fase casuale, tirano tutte in
direzioni diverse e in genere non produrranno un bel nulla
(o meglio produrranno un leggero rumore).
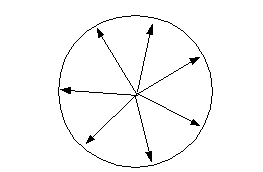
Oscillatori con fase
casuale
L'effetto non cambia se proviamo con un'altra frequenza e
un'altra ancora finché,sorpresa, per certe rare combinazioni
della lunghezza dell'onda e della distanza fra le pareti, le
frecce saranno tutte sovrapposte la loro somma sarà quindi
una freccia molto grande (figura sotto).
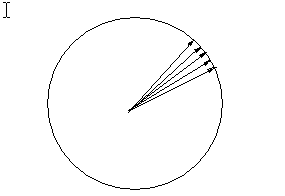
|
Oscillatori quasi in fase |
A queste particolari
frequenze dallo spettro si alzano alcuni sottili e altissimi
picchi : le frequenze proprie dell'oscillatore distribuito
nello spazio.
Chiameremo la prima da sinistra "fondamentale" e le altre
"armoniche".
Abbiamo quindi scoperto che gli oscillatori estesi nello
spazio non hanno una sola frequenza propria ma più frequenze
proprie.

|
Spettro dell'ampiezza di oscillazione in
funzione della frequenza |
Visto che la terminologia
ricorda la musica, guardiamo una corda di pianoforte
sollecitata da una sola delle frequenze proprie del suo
spettro.
Sotto sono riportati tre
casi: in ognuno si mostra la forma della corda che vibra su
e giù come un'onda stazionaria a 3 diverse frequenze proprie
di risonanza.
Nota che i tre casi sotto mostrati potevano essere
facilmente indovinati a partire dalle condizioni al
contorno: la corda di pianoforte è fissa agli estremi e lì
non può oscillare. A questo punto non devi fare altro che
cacciare nella corda tutte le forme d'onda che agli estremi
non vibrino. Funzionano tutte.

|
forme assunte dalla corda vincolata agli estremi
ad ognuna delle frequenze proprie |
Senza saperne di più
possiamo rispondere alla domanda: quante sono le frequenze
proprie ? Sono infinite perché alzando la frequenza di
queste combinazioni ne troviamo sempre altre. Quindi alla
fine avremo uno spettro con infiniti picchi gaussiani tutti
ben distinti e lontani fra loro.
Se esaminassimo l'energia cinetica associata ad ogni modo di
vibrazione noteremmo che, a parità di ampiezza, l'energia
legata alla fondamentale è più bassa delle altre perché la
corda si muove più lentamente.
Come già accaduto per l'altalena le frequenze proprie della
corda di pianoforte sono tutte quelle teoricamente possibili
ma non è detto che la corda stia vibrando.
Per farla vibrare occorre sollecitarla ad una delle
frequenze proprie e allora si avrà una risposta alla stessa
frequenza.
In realtà come sai la corda di pianoforte non viene
sollecitata con una sinusoide, viene solo battuta da un
martelletto, quindi le viene conferita energia in una forma
disordinata.
In questo caso la Natura deve decidere su quali frequenze
distribuire l'energia a disposizione. Ebbene la Natura
manifesta una preferenza per la nota fondamentale, quella a
più bassa energia. Pertanto verrà fuori una nota
fondamentale con grande ampiezza più le armoniche con
oscillazioni via via più piccoline. Questa somma di suoni è
il timbro del pianoforte (in realtà ci sarebbe anche la
vibrazione indotta nella cassa di legno ma lasciamo
perdere).
Se lo spettro si riferisce ad una struttura microscopica (ad
esempio ad un atomo) i picchi sono sottilissimi e altissimi
perchè a livello atomico l'attrito non esiste.
Io che sono una struttura macroscopica non vedo bene i
dettagli dello spettro.
Allora faccio una serie di affermazioni:
1- Un oscillatore non risponde ugualmente a qualunque
frequenza ma solo a certe particolari frequenze proprie
dettate dalle condizioni al contorno.
2 - La frequenza di un oscillatore è quantizzata, cioè non è
una variabile continua (come la lunghezza) ma assume solo
certi particolari valori.
Ambedue le affermazioni sono giuste ma la prima fa
riferimento al fenomeno ondulatorio così come effettivamente
avviene mentre la seconda introduce un modo di pensare a mio
avviso astratto e fuorviante, come se la Natura fosse
veramente discontinua (invece appare discontinua a me che
sono un po troppo voluminoso)
Ma quanti sono questi
oscillatori ? Non ci crederai ma al livello microscopico
pulsa tutto, ma proprio tutto. E' il modo di esprimersi
della Natura.
|

























.png)
































